In many papers, we can find the statements similar to the one below:
Because linear models can hardly capture the nonlinear relationship between load and temperature, we use Artificial Neural Networks (or other black-box models) in this paper.The major conceptual error of the above statement is due to a common misunderstanding that linear models cannot capture nonlinear relationship.
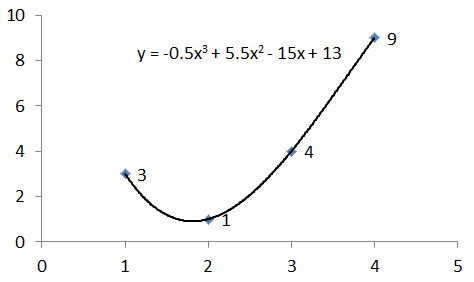
I'm showing a nonlinear curve in the figure below, which is from a 3rd order polynomial function.
Is this a linear model? Yes! Polynomial regression models in general are linear models.
Why?
The "linear" in linear models refers to the equations we use to solve the parameters. By definition, a regression model is linear if it can be written as Y = XB + E, where Y is a vector of values of the response variable; B is a vector of parameters to be solved; X is a matrix of values of explanatory variables; E is a vector of independent normally distributed errors.
Maybe the above description is too abstract. Let's check out an example of parameter estimation for a 3rd order polynomial regression model:
y = b0 + b1x1 + b2x2 + b3x3 + e,
where x2 is the square of x1, and x3 is the cube of x1. There are 4 parameters to be estimated. Now let's say we have 6 observations as shown in the table below.
Then we can come up with 6 linear equations:
3 = b0 + b1 + b2 + b3;
1 = b0 + 2b1 + 4b2 + 8b3;
4 = b0 + 3b1 + 9b2 + 27b3;
9 = b0 + 4b1 + 16b2 + 64b3;
5 = b0 + b1 + b2 + b3;
2 = b0 + 3b1 + 9b2 + 27b3;
These equations can be written in the following form:
Therefore, a 3rd order polynomial regression mode is a linear model. By solving the above equations, we can obtain the values of b0, b1, b2 and b3:
To further clarify the concept of linear vs. nonlinear, here are a few examples of nonlinear regression models:
y = b0 + b1x1/(b2x2 + b3) + e, ...... (1)
y = b0(exp(b1x))U, ...... (2)
Not to make it too complicated, some nonlinear regression problems can be solved in a linear domain. For instance, eq(2) can be transformed to a linear model by taking the logarithm on both side:
Ln(y) = Ln(b0) + b1x + u, .... (3)
Back to Load Forecasting Terminology.

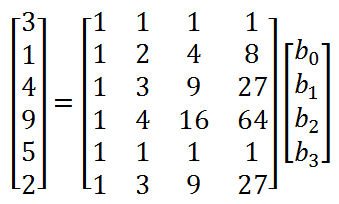

No comments:
Post a Comment
Note that you may link to your LinkedIn profile if you choose Name/URL option.